Wie man beurteilt, welche Rolle der Zufall in fairen Tests gespielt haben könnte
Bei der Auswertung der Ergebnisse fairer Therapievergleiche kann uns die Rolle, die der Zufall dabei spielt, dazu verleiten, zwei Arten von Fehlern zu begehen: Entweder wir kommen fälschlich zu dem Schluss, dass zwischen den Behandlungsergebnissen echte Unterschiede bestehen, wobei dies in Wirklichkeit gar nicht der Fall ist; oder wir folgern, dass sie sich nicht voneinander unterscheiden, obwohl es tatsächlich aber Unterschiede gibt. Je größer die Anzahl der beobachteten Behandlungsergebnisse, die uns interessieren, ist, desto geringer ist die Wahrscheinlichkeit, dass wir uns in der beschriebenen Art und Weise irren.
Da wir in Therapievergleichen nicht alle Menschen berücksichtigen können, die an der behandelten Krankheit leiden oder noch daran erkranken werden, lassen sich die «wahren Unterschiede» zwischen den untersuchten Therapien auch niemals endgültig feststellen. Stattdessen müssen Studien möglichst gute Schätzungen darüber abgeben, worin die wahren Unterschiede wahrscheinlich bestehen.
Die Zuverlässigkeit dieser geschätzten Unterschiede wird häufig als «Konfidenz- oder Vertrauensintervall» (engl. confidence interval, CI) angegeben. Diese Konfidenzintervalle geben den Bereich an, innerhalb dessen die wahren Unterschiede wahrscheinlich liegen. Den meisten Lesern ist das Konzept «Konfidenzintervall» bereits geläufig, wenn auch nicht unbedingt unter diesem Namen. Wir alle kennen Meinungsumfragen im Vorfeld von politischen Wahlen. Eine solche Umfrage könnte beispielsweise ergeben haben, dass Partei A 10 Prozentpunkte vor Partei B liegt; häufig wird in einer solchen Meldung dann darauf hingewiesen, dass der Unterschied zwischen den Parteien mindestens 5, höchstens aber bis zu 15 Prozentpunkte betragen könnte. Dieses «Konfidenzintervall» gibt an, dass der wahre Unterschied zwischen den Parteien wahrscheinlich irgendwo zwischen 5 und 15 Prozentpunkten liegt. Je größer die Anzahl der befragten Wähler, umso geringer ist die Unsicherheit bezüglich der Ergebnisse, und umso schmaler ist das zu dem geschätzten Unterschied gehörige Konfidenzintervall (Abb. 11).
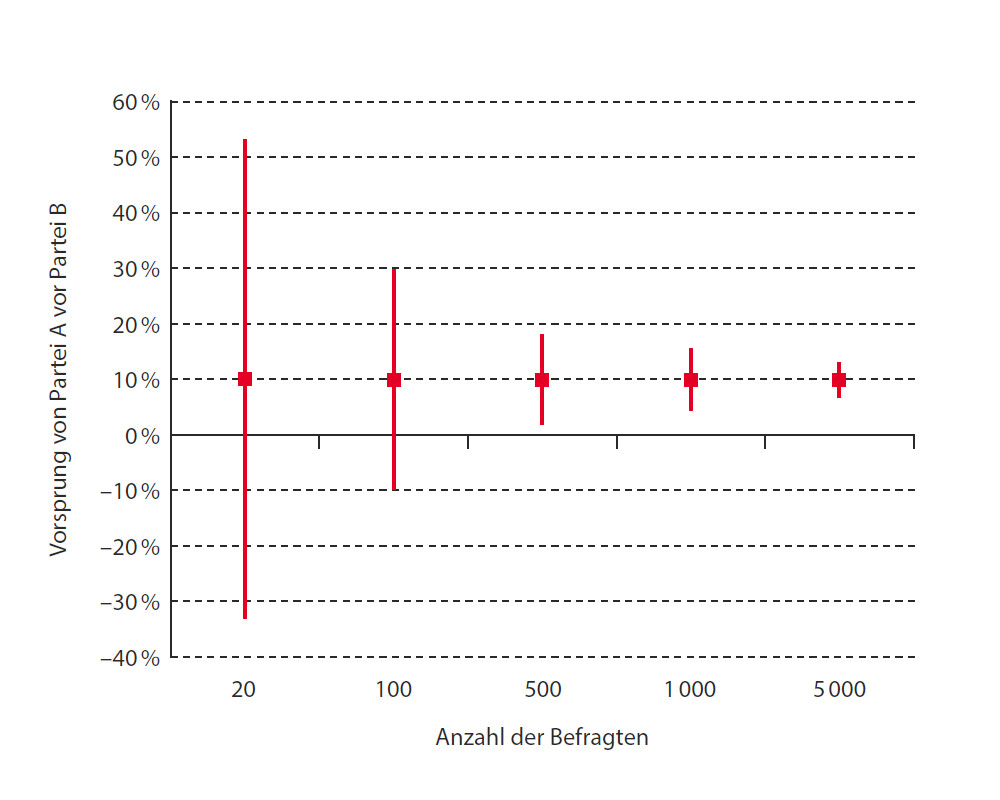
Abbildung 11: Das 95%-Konfidenzintervall (CI) für den Unterschied zwischen Partei A und Partei B wird mit zunehmender Anzahl der befragten Wähler schmaler.
Genauso wie man den Grad der Unsicherheit im Hinblick auf den geschätzten Unterschied in den Anteilen der Wähler bewerten kann, die zwei politische Parteien unterstützen, so lässt sich auch der Grad der Unsicherheit in Bezug auf den geschätzten Unterschied in den Anteilen der Patienten abschätzen, deren Zustand sich nach den zwei unterschiedlichen Therapien bessert oder verschlechtert. Auch hier heißt es: Je größer die Anzahl der untersuchten Behandlungsergebnisse – z. B. die Genesung nach einem Herzinfarkt – beim Vergleich zweier Therapien ist, umso schmaler werden auch die Konfidenzintervalle um die Schätzer der Therapieunterschiede sein. Für Konfidenzintervalle gilt: «Je schmaler, desto besser.»
Normalerweise wird bei einem Konfidenzintervall angegeben, wie sicher wir sein können, dass der wahre Wert innerhalb des angegebenen Schätzwertbereichs liegt. Ein «95 %-Konfidenzintervall» bedeutet beispielsweise, dass wir zu 95 % sicher sein können, dass der wahre Wert dessen, was geschätzt wird, innerhalb des durch das Konfidenzintervall eingegrenzten Bereichs liegt. Das heißt, es besteht eine Chance von 5 zu 100 (5 %), dass der «wahre» Wert tatsächlich außerhalb dieses Bereichs liegt.
